MHD natural convection
Taking advantage of our previous experience in natural convection and
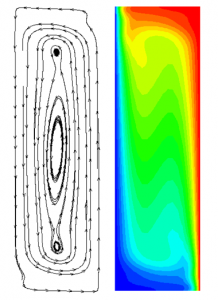heat transfer, we continue our research in MHD by studying problems in MHD natural convection of conducting fluids in rectangular and cylindrical domains. We have developed numerical models for the solution of both the full induction equations for the magnetic field and the low magnetic Reynolds number approximation, where the induced magnetic field is neglected. We have studied the damping effect of the magnetic field and its tendency to decelerate the fluid motion and to reduce the heat transfer from/to solid boundaries. Moreover, we have investigated the stabilization effect of the magnetic field to the onset of oscillatory flow in liquid metals. Reduction in heat transfer rate is unavoidable when a uniform magnetic field is imposed. However, for suitable sheared magnetic fields, the Lorentz force may accelerate the flow and we have considered models when such phenomena occur. We have also developed an appropriate numerical code and studied the natural convection of liquid metals between concentric isothermal cylinders subject to external magnetic fields.
MHD homogeneous turbulence
W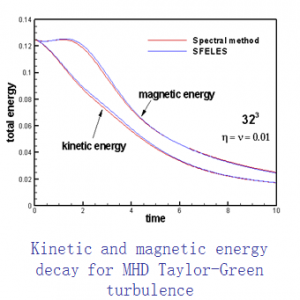
e have considering forced homogeneous MHD turbulence (Kolmogorov flow) in cubic boxes with periodic boundary conditions. The flow is driven by externally imposed shear magnetic fields. Direct and large eddy simulations are carried out in order to investigate the effect of Reynolds and magnetic Reynolds numbers to the statistically averaging velocity, magnetic field, magnetic stresses and Reynolds stresses of the turbulent MHD flows. The effect from the magnetic forcing is analysed and compared with the hydrodynamic analogue of the Kolmogorov flow. Results showed that for small but turbulent values of Reynolds number laminarization of the initial turbulent stage is observed. Thus, both flow and magnetic fields become steady and two-dimensional. On the contrary, for higher Reynolds numbers the flow remains turbulent. In the limit of low magnetic Reynolds numbers, a considerable decrease of magnetic fluctuations is observed.
LES of turbulent Hartmann flow
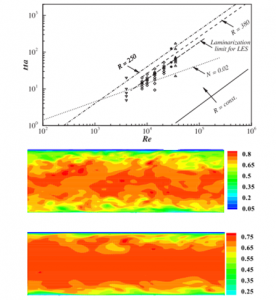Large-Eddy Simulations (LES) of turbulent and transitional channel flows of a conductive fluid under the effect of a uniform magnetic field applied in the wall-normal direction, usually referred to as Hartmann flows, are performed using the dynamic Smagorinsky model. The flow is characterized by the hydrodynamic Reynolds number R
e and the Hartmann number Ha that is related to the strength of the external magnetic field. Previous measurements and works on stability analysis have shown that a critical modified Reynolds number, based on the Hartmann laye
r thickness R=Re/Ha, exists at appro ximately R = 380. Here, the LES are used to investigate the laminarization of flow when decreasing R. Also, similarities of the turbulent flows are explored for different values of Re and Ha but the same values of R or of the interaction parameter N= Ha^2/Re. The LES confirm that R is the relevant parameter that describes the transition and a critical Reynolds number for re-laminarization is observed at R~500. However, for turbulent flows at moderate values of the Ha and Re as considered in this study, the similarity with respect to N appears to be better than for R, especially for the first order statistics. Finally, the importance of the dynamic Smagorinsky model as the Hartmann number increases is discussed.